Orthogonalizing EM

Orthogonalizing EM

oem(
  x,
  y,
  family = c("gaussian", "binomial"),
  penalty = c("elastic.net", "lasso", "ols", "mcp", "scad", "mcp.net", "scad.net",
    "grp.lasso", "grp.lasso.net", "grp.mcp", "grp.scad", "grp.mcp.net", "grp.scad.net",
    "sparse.grp.lasso"),
  weights = numeric(0),
  lambda = numeric(0),
  nlambda = 100L,
  lambda.min.ratio = NULL,
  alpha = 1,
  gamma = 3,
  tau = 0.5,
  groups = numeric(0),
  penalty.factor = NULL,
  group.weights = NULL,
  standardize = TRUE,
  intercept = TRUE,
  maxit = 500L,
  tol = 1e-07,
  irls.maxit = 100L,
  irls.tol = 0.001,
  accelerate = FALSE,
  ncores = -1,
  compute.loss = FALSE,
  hessian.type = c("upper.bound", "full")
)

Arguments

x	input matrix of dimension n x p or CsparseMatrix object of the Matrix package. Each row is an observation, each column corresponds to a covariate. The oem() function is optimized for n >> p settings and may be very slow when p > n, so please use other packages such as glmnet, ncvreg, grpreg, or gglasso when p > n or p approx n.
y	numeric response vector of length nobs.
family	"gaussian" for least squares problems, "binomial" for binary response.
penalty	Specification of penalty type. Choices include: "elastic.net" - elastic net penalty, extra parameters: "alpha" "lasso" - lasso penalty "ols" - ordinary least squares "mcp" - minimax concave penalty, extra parameters: "gamma" "scad" - smoothly clipped absolute deviation, extra parameters: "gamma" "mcp.net" - minimax concave penalty + l2 penalty, extra parameters: "gamma", "alpha" "scad.net" - smoothly clipped absolute deviation + l2 penalty, extra parameters: "gamma", "alpha" "grp.lasso" - group lasso penalty "grp.lasso.net" - group lasso penalty + l2 penalty, extra parameters: "alpha" "grp.mcp" - group minimax concave penalty, extra parameters: "gamma" "grp.scad" - group smoothly clipped absolute deviation, extra parameters: "gamma" "grp.mcp.net" - group minimax concave penalty + l2 penalty, extra parameters: "gamma", "alpha" "grp.scad.net" - group smoothly clipped absolute deviation + l2 penalty, extra parameters: "gamma", "alpha" "sparse.grp.lasso" - sparse group lasso penalty (group lasso + lasso), extra parameters: "tau" Careful consideration is required for the group lasso, group MCP, and group SCAD penalties. Groups as specified by the groups argument should be chosen in a sensible manner.
weights	observation weights. Not implemented yet. Defaults to 1 for each observation (setting weight vector to length 0 will default all weights to 1)
lambda	A user supplied lambda sequence. By default, the program computes its own lambda sequence based on nlambda and lambda.min.ratio. Supplying a value of lambda overrides this.
nlambda	The number of lambda values. The default is 100.
lambda.min.ratio	Smallest value for lambda, as a fraction of lambda.max, the (data derived) entry value (i.e. the smallest value for which all coefficients are zero). The default depends on the sample size nobs relative to the number of variables nvars. If nobs > nvars, the default is 0.0001, close to zero. If nobs < nvars, the default is 0.01. A very small value of lambda.min.ratio will lead to a saturated fit when nobs < nvars.
alpha	mixing value for elastic.net, mcp.net, scad.net, grp.mcp.net, grp.scad.net. penalty applied is (1 - alpha) * (ridge penalty) + alpha * (lasso/mcp/mcp/grp.lasso penalty)
gamma	tuning parameter for SCAD and MCP penalties. must be >= 1
tau	mixing value for sparse.grp.lasso. penalty applied is (1 - tau) * (group lasso penalty) + tau * (lasso penalty)
groups	A vector of describing the grouping of the coefficients. See the example below. All unpenalized variables should be put in group 0
penalty.factor	Separate penalty factors can be applied to each coefficient. This is a number that multiplies lambda to allow differential shrinkage. Can be 0 for some variables, which implies no shrinkage, and that variable is always included in the model. Default is 1 for all variables.
group.weights	penalty factors applied to each group for the group lasso. Similar to penalty.factor, this is a number that multiplies lambda to allow differential shrinkage. Can be 0 for some groups, which implies no shrinkage, and that group is always included in the model. Default is sqrt(group size) for all groups.
standardize	Logical flag for x variable standardization, prior to fitting the models. The coefficients are always returned on the original scale. Default is standardize = TRUE. If variables are in the same units already, you might not wish to standardize. Keep in mind that standardization is done differently for sparse matrices, so results (when standardized) may be slightly different for a sparse matrix object and a dense matrix object
intercept	Should intercept(s) be fitted (default = TRUE) or set to zero (FALSE)
maxit	integer. Maximum number of OEM iterations
tol	convergence tolerance for OEM iterations
irls.maxit	integer. Maximum number of IRLS iterations
irls.tol	convergence tolerance for IRLS iterations. Only used if family != "gaussian"
accelerate	boolean argument. Whether or not to use Nesterov acceleration with adaptive restarting
ncores	Integer scalar that specifies the number of threads to be used
compute.loss	should the loss be computed for each estimated tuning parameter? Defaults to FALSE. Setting to TRUE will dramatically increase computational time
hessian.type	only for logistic regression. if hessian.type = "full", then the full hessian is used. If hessian.type = "upper.bound", then an upper bound of the hessian is used. The upper bound can be dramatically faster in certain situations, ie when n >> p

Value

An object with S3 class "oem"

References

Shifeng Xiong, Bin Dai, Jared Huling, and Peter Z. G. Qian. Orthogonalizing EM: A design-based least squares algorithm. Technometrics, 58(3):285-293, 2016. http://amstat.tandfonline.com/doi/abs/10.1080/00401706.2015.1054436

Examples

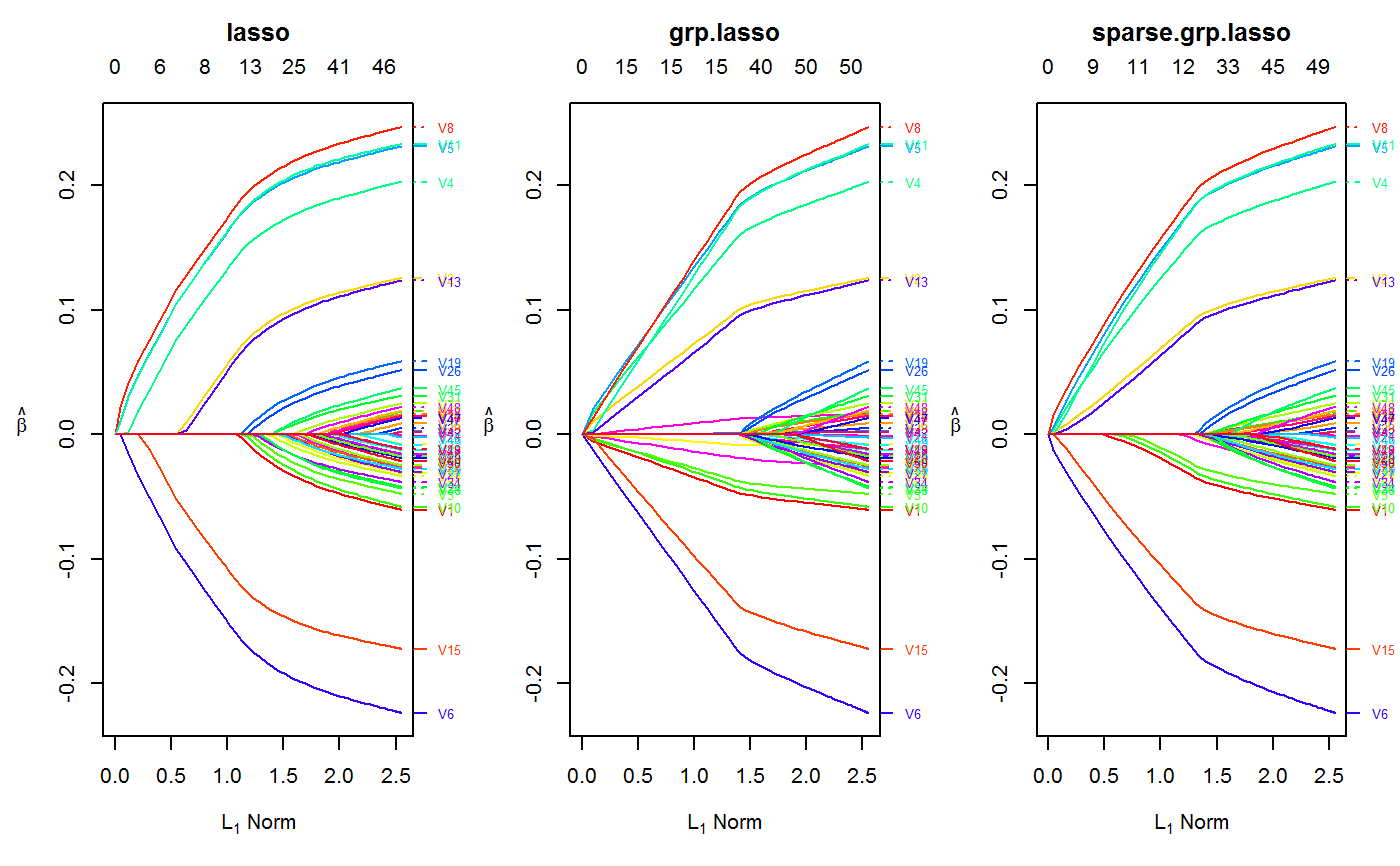
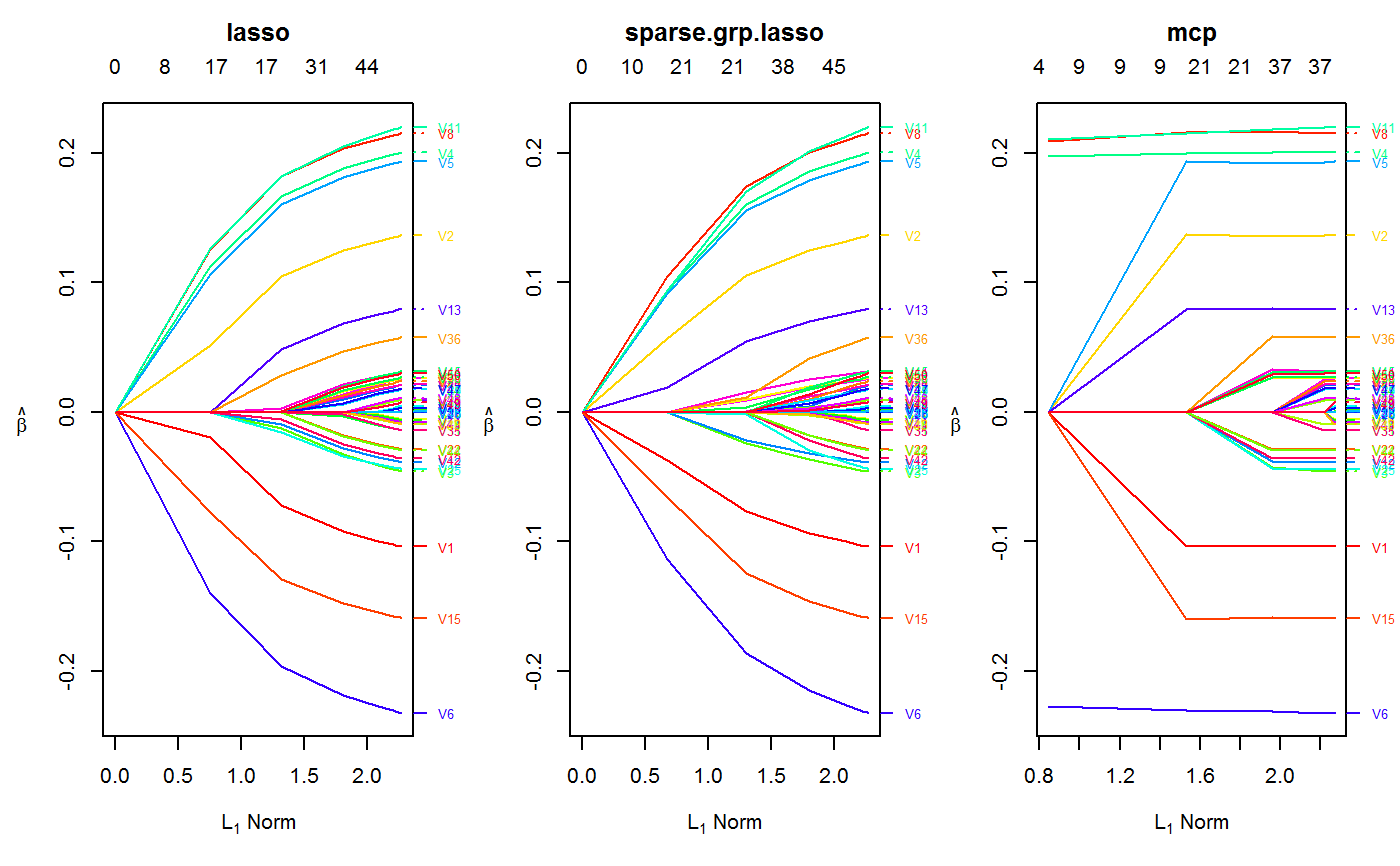
set.seed(123)
n.obs <- 1e4
n.vars <- 50

true.beta <- c(runif(15, -0.25, 0.25), rep(0, n.vars - 15))

x <- matrix(rnorm(n.obs * n.vars), n.obs, n.vars)
y <- rnorm(n.obs, sd = 3) + x %*% true.beta

fit <- oem(x = x, y = y,
           penalty = c("lasso", "grp.lasso", "sparse.grp.lasso"),
           groups = rep(1:10, each = 5))

layout(matrix(1:3, ncol = 3))
plot(fit)
plot(fit, which.model = 2)
#> Warning: collapsing to unique 'x' values
plot(fit, which.model = "sparse.grp.lasso")
#> Warning: collapsing to unique 'x' values

# the oem package has support for
# sparse design matrices

library(Matrix)

xs <- rsparsematrix(n.obs * 25, n.vars * 2, density = 0.01)
ys <- rnorm(n.obs * 25, sd = 3) + as.vector(xs %*% c(true.beta, rep(0, n.vars)) )
x.dense <- as.matrix(xs)

system.time(fit <- oem(x = x.dense, y = ys,
                       penalty = c("lasso", "grp.lasso"),
                       groups = rep(1:20, each = 5), intercept = FALSE,
                       standardize = FALSE))
#>    user  system elapsed 
#>   25.91    0.14   27.37 

system.time(fits <- oem(x = xs, y = ys,
                        penalty = c("lasso", "grp.lasso"),
                        groups = rep(1:20, each = 5), intercept = FALSE,
                        standardize = FALSE, lambda = fit$lambda))
#>    user  system elapsed 
#>    0.56    0.00    0.71 

max(abs(fit$beta[[1]] - fits$beta[[1]]))
#> [1] 1.582068e-15
max(abs(fit$beta[[2]] - fits$beta[[2]]))
#> [1] 1.609823e-15

# logistic
y <- rbinom(n.obs, 1, prob = 1 / (1 + exp(-x %*% true.beta)))

system.time(res <- oem(x, y, intercept = FALSE,
                       penalty = c("lasso", "sparse.grp.lasso", "mcp"),
                       family = "binomial",
                       groups = rep(1:10, each = 5),
                       nlambda = 10,
                       irls.tol = 1e-3, tol = 1e-8))
#>    user  system elapsed 
#>    3.98    0.03    4.30 

layout(matrix(1:3, ncol = 3))
plot(res)
plot(res, which.model = 2)
plot(res, which.model = "mcp")


# sparse design matrix
xs <- rsparsematrix(n.obs * 2, n.vars, density = 0.01)
x.dense <- as.matrix(xs)
ys <- rbinom(n.obs * 2, 1, prob = 1 / (1 + exp(-x %*% true.beta)))

system.time(res.gr <- oem(x.dense, ys, intercept = FALSE,
                          penalty = "grp.lasso",
                          family = "binomial",
                          nlambda = 10,
                          groups = rep(1:5, each = 10),
                          irls.tol = 1e-3, tol = 1e-8))
#>    user  system elapsed 
#>    1.97    0.03    2.11 

system.time(res.gr.s <- oem(xs, ys, intercept = FALSE,
                            penalty = "grp.lasso",
                            family = "binomial",
                            nlambda = 10,
                            groups = rep(1:5, each = 10),
                            irls.tol = 1e-3, tol = 1e-8))
#>    user  system elapsed 
#>    0.59    0.00    0.69 

max(abs(res.gr$beta[[1]] - res.gr.s$beta[[1]]))
#> [1] 6.647085e-05